COMPOSITIE – REGEL VAN DERDEN & DE GULDEN SNEDE
Door bij het te schilderen beeld rekening te houden met een juiste compositie heb je al heel veel gewonnen. Je kunt je standpunt zo kiezen dat het beeld interessanter lijkt. De verschillende onderdelen in het beeld zijn zo geplaatst dat ze één samenhangend mooi geheel vormen. Het moet voor de kijker fijn zijn om naar het beeld te kijken waarbij de essentiële onderdelen van “het verhaal” automatisch de aandacht trekken.
In de schilderkunst worden hierbij twee methoden gehanteerd, namelijk:
- De Regel van Derden
- De Gulden Snede.
Hieronder vindt je uitleg en voorbeelden.
Opmerking: Bij het schilderen komt het allemaal niet zo precies. Je kunt heel veel op gevoel doen. Het is ook een enorm gereken. Ik heb daarom een excel-programmatje gemaakt. Je vult de breedtemaat en hoogtemaat van je schilderij in en de coördinaten voor beide methoden “rollen er zo uit”. Heb je hiervoor belangstelling, stuur me dan even een e-mailbericht.
De Regel van Derden:
Bij de regel van derden wordt het beeld zowel in de breedte als de hoogte in drie gelijke delen ingedeeld. Zodoende ontstaan er in het beeld vier coördinaten. Op deze coördinaten plaats je de blikvangers zoals een persoon in een landschap, het rode dak van een boerderij, de ogen van de kat. De horizon van het landschap plaats je op 1/3 of 2/3 van de hoogte.
Voorbeeld van De Regel van Derden:
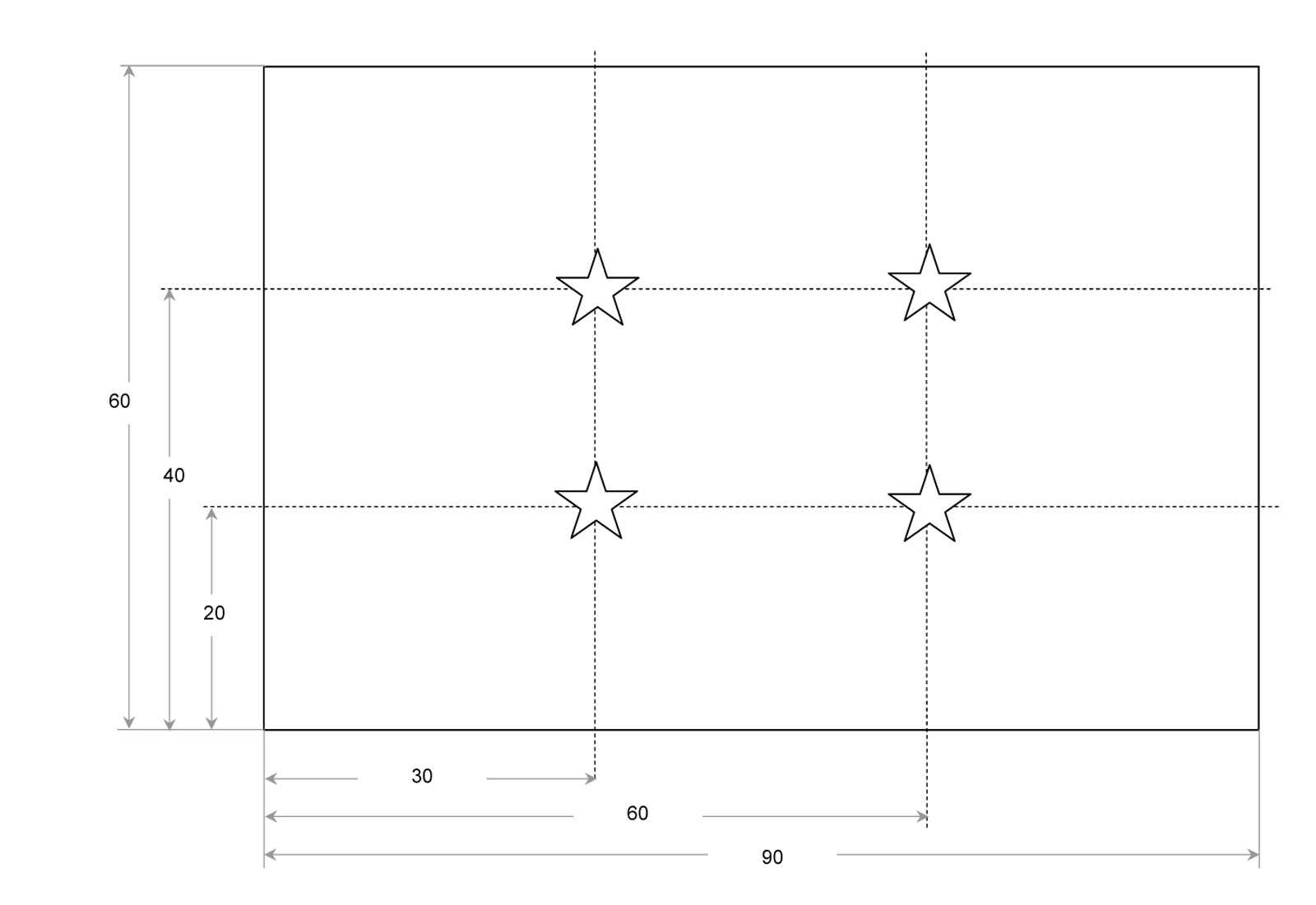
Het schilderij heeft een breedte van 90cm en een hoogte van 60 cm. De breedte wordt ingedeeld in drieën. Je tekent twee verticale lijnen op de breedtecoördinaten van 30 en 60 cm. De hoogte wordt ingedeeld in drieën. Je tekent twee horizontale lijnen op de hoogtecoördinaten van 20 en 40 cm. De vier b/h-coördinaten (de snijpunten van de verticale en horizontale lijnen) bevinden zich respectievelijk op: 30/20 – 30/40 – 60/20 – 60/40 (cm/cm). Zie tekening.
Voorbeeld: Maatverdeling De Regel van Derden
Schilderij: Het rood/witte treintje en verdwijnpunt op een coördinaat volgens De Regel van Derden.
De Gulden Snede:
De gulden snede bezit volgens sommigen een intrinsieke schoonheid waardoor die verhouding veel voorkomt in klassieke architectuur en schilderkunst (Wikipedia). Bij de gulden ontstaan eveneens vier hoofdcoördinaten. Ook nu wordt de breedte en hoogte in drieën verdeeld. Echter niet in gelijke delen, zoals bij de regel van derden, maar volgens een bepaalde mathematische (wiskundig berekende) verhouding. Dit verhoudingsgetal (phi) noemen we het Gulden Getal. Afgerond is phi 1,618.
Voorbeeld van De Gulden Snede:
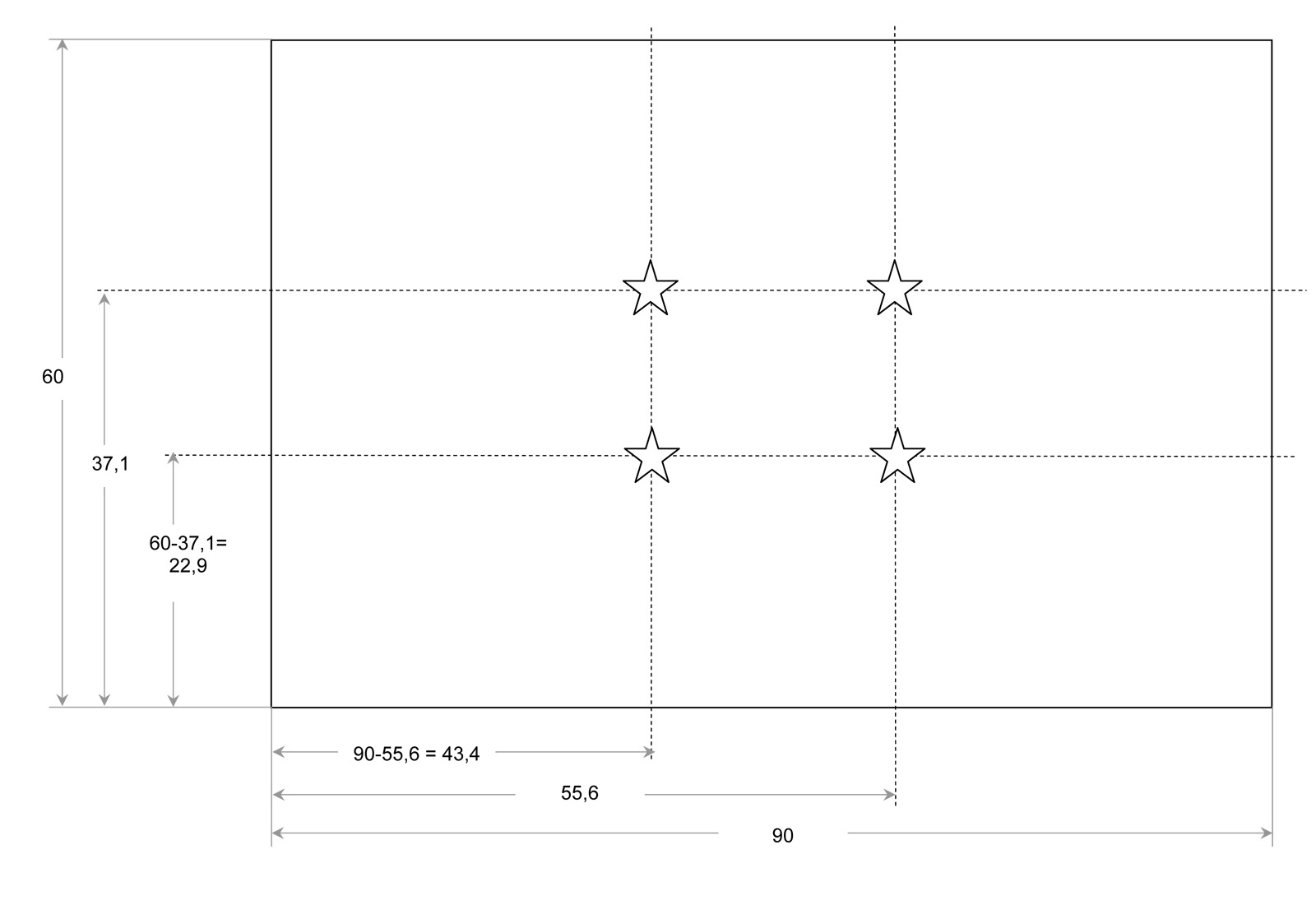
Het schilderij heeft een breedte van 90cm en een hoogte van 60 cm. De breedte wordt ingedeeld in twee delen volgens het Gulden Getal phi (1,618). In ons voorbeeld: 90 cm/1,618= 55,6 cm. Je tekent een verticale lijn op het breedtecoördinaat 55,6 cm. De hoogte wordt eveneens ingedeeld in twee delen volgens het Gulden Getal phi. In ons voorbeeld: 60 cm/1,618 = 37,1 cm. Je tekent een horizontale lijn op het hoogtecoördinaat 37,1. Het b/h-coördinaat (het snijpunt van de verticale en horizontale lijn) bevindt zich op 55,6/37,1 (cm/cm). Op deze manier bepaal je van recht-links/links-rechts/onder/boven, boven/onder vier coördinaten. Zie tekening.
Voorbeeld: Maatverdeling De Gulden Snede
Schilderij: Het doorkijkje is de blikvanger en bevindt zich op een coördinaat volgens De Gulden Snede